TEMA 1
Principio de Pascal
La presión es la eficiencia de una cierta fuerza a menudo depende del área sobre la que actúa.
la presión P está dada por la ecuación:
la diferencia que hay entre cómo actúa la fuerza de un fluido y como lo hace sobre un sólido es que el sólido es un cuerpo rígido, puede soportar que se le aplique una fuerza sin cambiar apreciablemente su forma, y un líquido puede soportar una fuerza únicamente en un superficie o frontera cerrada.
Presión hidrostática, considerando la densidad
del líquido y la profundidad a la que se encuentre el punto.
La
mayoría de los dispositivos que permiten medir la presión directamente miden en
realidad la diferencia entre la presión absoluta y la presión atmosférica. El
resultado obtenido se conoce como la presión manométrica.
Presión absoluta = Presión manométrica +
Presión atmosférica
Ejercicios
Aplicaciones en
la vida cotidiana
la prensa hidráulica, consta esencialmente de
dos cilindros de diferente diámetro, cada uno con su respectivo émbolo, unidos
por medio de un tubo de comunicación. Se llenan de líquido el tubo y los
cilindros, y al aplicar una fuerza en el émbolo de menor tamaño la presión que
genera se transmite íntegramente al émbolo mayor. Al penetrar el líquido en el
cilindro mayor, unido a una plataforma, el líquido empuja el émbolo hacia
arriba.
-La prensa
hidráulica se utiliza en:
-Estaciones de
servicio para levantar automóviles
-Para comprimir
algodón o tabaco
-Para extraer
aceite de algunas semillas, o jugos de algunas frutas
-Los frenos
hidráulicos de los automóviles
La presión en el
émbolo menor está dada por la relación de la fuerza (F1) entre el área (A1) y
en el émbolo mayor por la relación de la fuerza (F2) entre el área (A2).
Ejercicios
TEMA 2
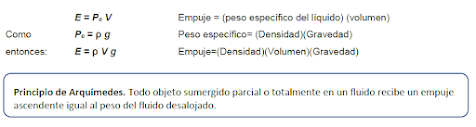
Principio de Arquímedes
El
principio de Arquímedes es el principio físico que afirma: «Un cuerpo total o
parcialmente sumergido en un fluido en reposo experimenta un empuje vertical
hacia arriba igual al peso del fluido desalojado». Esta fuerza recibe el
nombre de empuje hidrostático o de Arquímedes, y se mide en newtons.
TEMA 3
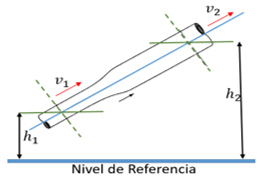
Ecuación de continuidad
Ecuación de Continuidad, que se basa principalmente en un tubo de secciones transversales diferentes, como el que se muestra en la imagen, el gasto que fluye por la sección transversal 1, es igual al gasto que fluye por la sección transversal 2, es decir, la cantidad de líquido que pasa por 1 y 2 es la misma.
La fórmula es la siguiente:
Dónde:
A1 =
área de la sección transversal en el punto 1
A2 = área
de la sección transversal en el punto 2
V1 = velocidad
del líquido en el punto 1
V2= velocidad
del líquido en el punto 2
Ejercicios
Problema
1.- Por una tubería de 0.11 m de diámetro circula agua a una velocidad de
3 m/s ¿cuál es la velocidad que llevará el agua, al pasar por un estrecho de la
tubería donde el diámetro es de 0.04 m?
Solución: Vamos a considerar a nuestros datos para poder facilitarnos el cálculo.
V1 =
3m/s Si analizamos nuestra
fórmula:
D = 0.11 m Despejando a “v2”, obtenemos:
d =
0.04 m
v2 =? pidan áreas y no diámetros, podemos hacer la relación siguiente.
Podemos simplificar en la parte del numerador con el denominador a π/4, entonces:
Ahora, sustituyendo:
resultado:
Obtenemos una velocidad de 22.68 m/s
Ejemplo 2.- Por una manguera de bomberos de
0.25 metros de diámetro sale a presión agua que fluye a una velocidad de 10.5
m/s, si la manguera se achica en su boquilla de salida a 0.1 metros de diámetro
¿con qué velocidad saldrá el chorro?
Solución:
Nuevamente recolectamos los datos del
problema.
TEMA 4
Teorema de Bernoulli
El teorema de Bernoulli, también conocido como el principio de Bernoulli; una postulación del científico suizo Daniel Bernoulli.
Este enunciado se enfoca en probar el comportamiento de un fluido que circula en una línea de corriente. Se establece que el fluido ideal no posee ningún tipo de viscosidad, y no está sometido a fricción. Así mismo, al encontrarse en circulación dentro de un conducto cerrado, si se cumplen estas características, su energía permanecerá constante.
La aplicación de este teorema se ha relacionado estrechamente con la ingeniería. Y puede ser usado para el estudio de distintos tipos de fluidos, por lo que se han detallado distintas formas de la ecuación de Bernoulli.
¿Qué
es el teorema de Bernoulli?
Ecuación
del teorema de Bernoulli
Teniendo
en cuenta la teoría, se tiene que el teorema trabajo únicamente con tres tipos
de energía:
Cinética: hace referencia a la velocidad que posee un fluido.
Potencial:
relacionada con la altitud que posee un fluido.
De
presión: equivale a la energía de un fluido resultado de la presión a la que
está sometido.
Definiendo las variables:
V =
velocidad del fluido
p =
densidad del fluido
P =
presión del fluido en la línea de corriente
g =
aceleración gravitatoria
z =
altura en la dirección de la gravedad
Restricciones
de la Ecuación de Bernoulli
Aunque
la ecuación de Bernoulli se aplica a muchos problemas prácticos, o ejemplos hay
ciertas limitaciones que se deben de considerar, a fin de aplicarse con la
propiedad adecuada.
1.-
Es válida solamente para fluidos incompresibles, ya que el peso específico del
fluido permanece constante en la sección inicial y final.
2.-
No puede haber sistemas mecánicos que agreguen o retiren energía del sistema
entre la sección inicial y final, ya que la energía del sistema permanece
constante.
3.-
Al igual que el punto dos, no puede haber transferencia de calor hacia el
fluido o fuera de éste.
4.-
No debe considerarse la pérdida de energía debido a la fricción.
Ejercicios
Problema
1: Un flujo de agua va de la sección 1 a la seccion 2. La sección 1 tiene 25 mm
de diámetro, la presión manométrica es de 345 kPa, y la velocidad de flujo es
de 3 m/s. La sección 2, mide 50 mm de diámetro, y se encuentra a 2 metros por
arriba de la sección 1. Si suponemos que no hay pérdida de energía en el
sistema. Calcule la presión “P2”
Solución:
Tenemos que analizar nuestros datos, es decir, que es lo qué si tenemos y lo que nos hace falta por encontrar, así también realizar el despeje de la variable que vamos a calcular. Entonces procedemos:
Datos:
d1 = 25 mmd2 = 50 mm
p1
=345 Kpa
v1 =
3 m/s
d2 =
50 mm
p2 =?
Si leemos bien el problema, nos daremos cuenta que tenemos la altura, ya que si hacemos h2 – h1 = 2 metros. Por lo que nos ahorramos algo de cálculo. Finalmente procedemos a despejar a p2 de la fórmula que ya tenemos:
Despejando y para hacer más fácil el proceso, recordemos que la densidad del agua no tendrá ninguna variación tanto al inicio como al final, entonces podemos decir que la densidad será constante, y la podemos omitir para el cálculo.
Sin
embargo nos hace falta v2, ya que no la tenemos, pero si tenemos el dato de los
diámetros, entonces si recordamos bien; podemos hacer uso de la ecuación de
continuidad qué es una ecuación que
deriva del gasto
Así
que:
A1V1=
A2V2
Despejamos
“V2”
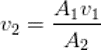
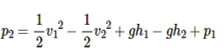
No hay comentarios.:
Publicar un comentario